定义

状态压缩动态规划，简称 状压 dp，通过二进制 将状态压缩为整数 来达到优化转移的目的

一个简单的例子

对于一个 01 背包（大家都会对吧）

有 $n\leq 15$ 件物品和一个容量无限大的背包，第 $i$ 件物品所占空间为 $w_i$ ，价值为 $v_i$ ，求每种放法的价值和占用的空间

1.定义状态

我们要求每种放法的价值，且对于一个 01 背包的每个物品都只有放与不放两种情况

于是我们定义的状态应是这 $n$ 件物品放与不放的情况

容易想到我们可以开个 $n$ 维数组，第 $i$ 个维度的下标如果是 $1$ 则代表放第 $i+1$ 件物品， 反之则不放

假设我们有 $5$ 件物品， 那么 $dp[1][0][1][1][0]$ 则代表放第 $1,3,4$ 件物品可以获得的价值

但你愿意一个维度一个维度地开吗？（）

我们发现对于这个问题可以用二进制来表示所有情况，如果我们将其转化为十进制就可以用 $1$ 个维度来表达刚才 $n$ 个维度所表达的信息

例如刚才我们显然可以用 $00000\thicksim 11111$ 来表示所有情况，转化为十进制就是 $0\thicksim (1<<5-1)$

2.如何转移

放的状态只能由不放的状态转移而来

例如$dp[10000_{(2)}]=dp[00000_{(2)}]+v[1]$，$dp[11000_{(2)}]=dp[10000_{(2)}]+v[2]=dp[01000_{(2)}]+v[1]$

3.代码

#include<cstdio>

int dp[2][(1 << 15) + 5]; //dp[0]为价值,dp[1]为空间
int n, w[20], v[20];

void print(int s);

int main() {
	scanf("%d", &n);
	for(int i = 0; i < n; ++i) scanf("%d%d", &w[i], &v[i]);
	for(int i = 0; i < (1 << n); ++i) {
		for(int j = 0; j < n; ++j) {
			if(!(i & (1 << j))) {
				dp[0][i | (1 << j)] = dp[0][i] + v[j];
				dp[1][i | (1 << j)] = dp[1][i] + w[j];
			}
		}
	}
	for(int i = 0; i < (1 << n); ++i) {
		print(i);
		printf("\t%d\t%d\n", dp[0][i], dp[1][i]);
	}
	return 0;
}

void print(int s) {
	if(!s) printf("0");
	int k = 0;
	for(; (1 << k) <= s; ++k) {
		if(s & (1 << k)) printf("1");
		else printf("0");
	}
}

/*
3
2 5
3 8
4 9
*/ //一组样例
/*
0       0       0
1       5       2
01      8       3
11      13      5
001     9       4
101     14      6
011     17      7
111     22      9
*/

互不侵犯

在 $N\times N$ 的棋盘里面放 $K$ 个国王，使他们互不攻击，共有多少种摆放方案？

国王能攻击到它上下左右，以及左上左下右上右下八个方向上附近的各一个格子，共 $8$ 个格子

solution

我们定义 $dp[i][j][l]$ 表示前 $i$ 行，第 $i$ 行的状态为 $j$ ，且棋盘上已经放了 $l$ 个国王时的合法方案数

对于每个状态 $j$ ，其二进制位上为 $1$ 则代表那个位上放置国王，反之则不放

例如下图 $j=101001_{(2)}$ ，$sta[j]=3$

img

设当前行状态为 $j$ ，上一行状态为 $k$ ，在保证当前行和上一行不冲突的前提下，枚举所有可能的 $k$ 进行转移，有转移方程

$$f[i][j][l]=\sum f[i-1][k][l-bitcount(j)]$$

代码

#include<cstdio>

int n, p;
long long dp[11][(1 << 9) + 5][101], ans;
int bitcount[(1 << 9) + 5];

int main() {
	scanf("%d%d", &n, &p);
	dp[0][0][0] = 1;
	for(int i = 0; i < (1 << n); ++i) {
		int t = i;
		while(t) {
			if(t & 1) ++bitcount[i];
			t >>= 1;
		}
	}
	for(int i = 1; i <= n; ++i) {
		for(int j = 0; j < (1 << n); ++j) {
			if(!(j & (j << 1 | j >> 1))) {
				for(int k = 0; k < (1 << n); ++k) {
					if(!(j & (k | k << 1 | k >> 1))) {
						for(int l = bitcount[k]; l <= p; ++l) {
							dp[i][j][l] += dp[i - 1][k][l - bitcount[j]];
						}
					}
				}
			}
		}
	}
	for(int i = 0; i < (1 << n); ++i) ans += dp[n][i][p];
	printf("%lld\n", ans);
	return 0;
}

炮兵阵地

司令部的将军们打算在 $N\times M$ 的网格地图上部署他们的炮兵部队。

一个 $N\times M$ 的地图由 $N$ 行 $M$ 列组成，地图的每一格可能是山地（用 $\texttt{H}$ 表示），也可能是平原（用 $\texttt{P}$ 表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

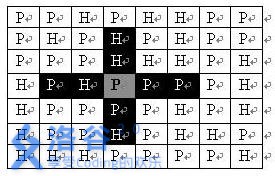
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

solution

我们定义 $dp[l][s][i]$ 表示上一状态为 $l$，当前状态为 $s$，当前考虑到第 $i$ 行时最多放置的炮兵数，$bin[i]$ 表示第 $i$ 行的地形情况

然后我们发现对于每一行 $i$，只需要 $i,i-1,i-2$ 三行，于是考虑使用滚动数组进行优化（否则$MLE\ \ 0$）

与互不侵犯相同，对于每个状态 $l$（或 $s$），二进制位上为 $1$ 则代表放置炮兵，反之不放

设上上行状态为 $j$ ，在满足题目要求的前提下，有转移方程

$$dp[l][s][i]=max(dp[j][l][(i-1)])+bitcount(s)$$

代码

#include<cstdio>

int dp[(1 << 10) + 5][(1 << 10) + 5][3], bin[105], bitcount[(1 << 10) + 5];
int n, m, ans;

inline int max(const int &a, const int &b) {return a > b ? a : b;}

int main() {
	scanf("%d%d", &n, &m);
	for(int i = 0; i < (1 << m); ++i) {
		int t = i;
		while(t) {
			if(t & 1) ++bitcount[i];
			t >>= 1;
		}
	}
	for(int i = 0, x; i < n; ++i) {
		for(int j = 0; j < m; ++j) {
			scanf(" %c", &x);
			if(n == 1 && m == 1 && x == 'P') {
				printf("1\n");
				return 0;
			}
			bin[i] = (bin[i] << 1) | x == 'H';
		}
	}
	for(int l = 0; l < (1 << m); ++l) {
		for(int s = 0; s < (1 << m); ++s) {
			if(!((l & (s | bin[0] | (l << 1) | (l << 2))) || (s & (bin[1] | (s << 1) | (s << 2))))) {
				dp[l][s][1] = bitcount[s] + bitcount[l];
			}
		}
	}
	for(int i = 2; i < n; ++i) {
		for(int l = 0; l < (1 << m); ++l) {
			if(!(l & (bin[i - 1] | (l << 1) | (l << 2)))) {
				for(int s = 0; s < (1 << m); ++s) {
					if(!(s & (bin[i] | (s << 1) | (s << 2) | l))) {
						for(int j = 0; j < (1 << m); ++j) {
							if(!(j & (bin[i - 2] | (j << 1) | (j << 2) | s | l))) {
								dp[l][s][i % 3] =
                                    max(dp[l][s][i % 3], dp[j][l][(i - 1) % 3] + bitcount[s]);
							}
						}
					}
				}
			}
		}
	}
	for(int l = 0; l < (1 << m); ++l) {
		for(int s = 0; s < (1 << m); ++s) {
			ans = max(ans, dp[l][s][(n - 1) % 3]);
		}
	}
	printf("%d\n", ans);
	return 0;
}

玉米田

农场主 John 新买了一块长方形的新牧场，这块牧场被划分成 $M$ 行 $N$ 列($1 ≤ M ≤ 12; 1 ≤ N ≤ 12$)，每一格都是一块正方形的土地。John 打算在牧场上的某几格里种上美味的草，供他的奶牛们享用。

遗憾的是，有些土地相当贫瘠，不能用来种草。并且，奶牛们喜欢独占一块草地的感觉，于是 John 不会选择两块相邻的土地，也就是说，没有哪两块草地有公共边。

John 想知道，如果不考虑草地的总块数，那么，一共有多少种种植方案可供他选择？（当然，把新牧场完全荒废也是一种方案）

solution

相信你已经找到套路了对吧（确信

我们定义 $dp[i][j]$ 表示前 $i$ 行且第 $i$ 行状态为 $j$ 的方案数，$bin[i]$ 第 $i$ 行的地形情况 （熟悉吗）

与前面同样的，对于每个状态 $j$ ，二进制位上为 $1$ 则代表种草，反之不种

仍然同样的，设当前行状态为 $j$ ，上一行状态为 $k$ ，在满足题目要求的前提下，有转移方程

$$dp[i][j]=\sum dp[i-1][k]$$

代码

#include<cstdio>

const int MOD = 100000000;
int dp[15][(1 << 12) + 5], bin[15];
int n, m, ans;

int main() {
	scanf("%d%d", &n, &m);
	for(int i = 0, x; i < n; ++i) {
		for(int j = 0; j < m; ++j) {
			scanf("%d", &x);
			bin[i] = (bin[i] << 1) | !x;
		}
	}
	for(int i = 0; i < (1 << m); ++i) {
		if(!(i & (bin[0] | (i << 1)))) {
			dp[0][i] = 1;
		}
	}
	for(int i = 1; i < n; ++i) {
		for(int j = 0; j < (1 << m); ++j) {
			if(!(j & (bin[i] | (j << 1)))) {
				for(int k = 0; k < (1 << m); ++k) {
					if(!(k & (bin[i - 1] | (k << 1) | j))) {
						dp[i][j] = (dp[i][j] + dp[i - 1][k]) % MOD;
					}
				}
			}
		}
	}
	for(int i = 0; i < (1 << m); ++i) {
		ans = (ans + dp[n - 1][i]) % MOD;
	}
	printf("%d\n", ans);
}

更新日志

2025/10/12 07:02

查看所有更新日志

• 7ced7-Reuploads previous blogs于 2025/10/12

版权所有

许可证：署名-非商业性-相同方式共享 4.0 国际 (CC-BY-NC-SA-4.0)