斜率优化dp入门
前置知识
| 名称 | 定义 |
|---|---|
| 凸多边形 | 所有内角都在(0°,180°)的简单多边形 |
| 凸包 | 在平面上能包含所有给定点的最小凸多边形叫做凸包。 |
| 上凸包 | 凸包中横坐标最小的点到横坐标最大的点的上半部分 |
| 下凸包 | 凸包中横坐标最小的点到横坐标最大的点的下半部分 |
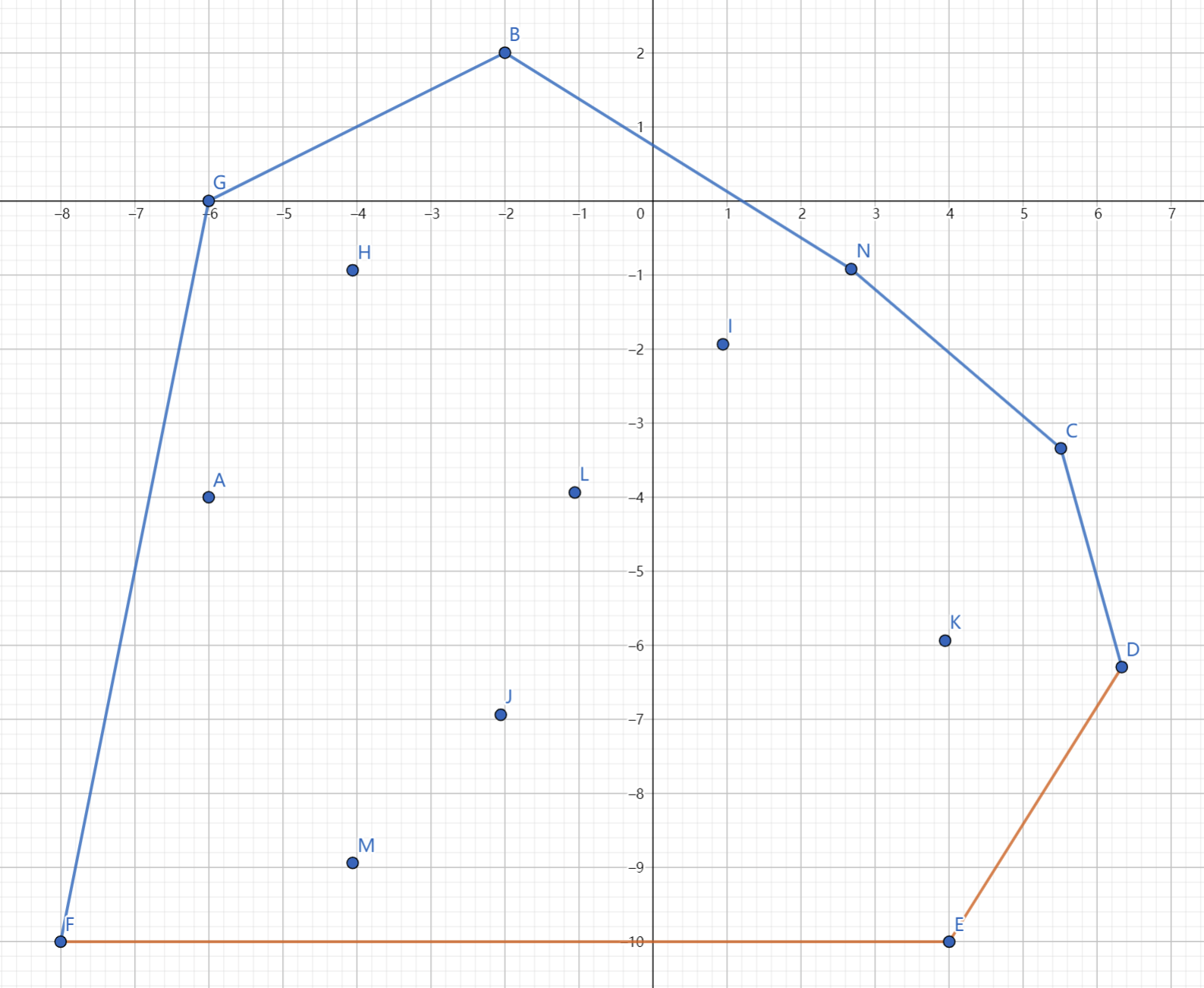
如右图,蓝色部分是上凸包,橙色部分是下凸包
让我们通过例题来学习斜率优化dp
例题
[HNOI2008] 玩具装箱
题目描述
P 教授要去看奥运,但是他舍不下他的玩具,于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩,其可以将任意物品变成一堆,再放到一种特殊的一维容器中。
P 教授有编号为 1⋯n 的 n 件玩具,第件玩具经过压缩后的一维长度为 Ci。
为了方便整理,P 教授要求:
- 在一个一维容器中的玩具编号是连续的。
- 同时如果一个一维容器中有多个玩具,那么两件玩具之间要加入一个单位长度的填充物。形式地说,如果将第 i 件玩具到第 j 个玩具放到一个容器中,那么容器的长度将为 x=j−i+∑k=ijCk。
制作容器的费用与容器的长度有关,根据教授研究,如果容器长度为 x,其制作费用为 (x−L)2。其中 L 是一个常量。P 教授不关心容器的数目,他可以制作出任意长度的容器,甚至超过 L。但他希望所有容器的总费用最小。
输入格式
第一行有两个整数,用一个空格隔开,分别代表 n 和 L。
第 2 到 第 (n+1) 行,每行一个整数,第 (i+1) 行的整数代表第 i 件玩具的长度 Ci。
输出格式
输出一行一个整数,代表所有容器的总费用最小是多少。
数据范围
对于全部的测试点,1≤n≤5×104,1≤L≤107,1≤Ci≤107
基本dp思路
设Fi为装前i个玩具的最小费用,则Fi=min0≤j<i(Fj+(i−j−1−L+∑k=j+1iCk)2)
其中∑k=j+1iCk可以用前缀和优化掉,变成Fi=min0≤j<i(Fj+(i−j−1−L+sumi−sumj)2)
非常好啊,O(n2),0 分到手
怎么办呢?
处理一下
这个dp方程好像不太好处理
首先我们不看这个min,只看Fi=Fj+(i−j−1−L+sumi−sumj)2
令A=i+sumi,BFj+(A−B−C)2Fi+2A(B+C)令x=B+C,y=Fjy=j+sumj,C=L+1=Fj+A2+(B+C)2−2A(B+C)=Fj+A2+(B+C)2+(B+C)2,k=2A,b=Fi−A2=kx+b
想到了什么?
我们要最小化Fi,那也就是说我们要最小化b
对于每一个确定的i,k都是确定的
问题转化成了求过(B+C,Fj+(B+C)2)中任意一点且斜率为 k 的直线截距的最小值。
补充知识
如果你只想知道斜率优化怎么用,那么你可以点此跳过这部分。
我们易可证截距的最小值一定取在下凸包上
证明:假如截距的最小值取在非下凸包上的一个点(x0,y0),则有两种情况:
(一) 下凸包上有一个点(x0,y1)
所以过(x0,y0)的直线的解析式为y=kx+y0−kx0,过(x0,y1)的直线的解析式为y=kx+y1−kx0
根据下凸包的定义可得y0>y1,故y0−kx0>y1−kx1,矛盾
(二) 下凸包上没有和其横坐标相同的点
根据下凸包的定义,可得下凸包上一定存在两个点(x1,y1),(x2,y2)使得x1<x0<x2且x0x1−x2y1−y2+x1−x2x1y2−x2y1<y0
我们在经过(x1,y1), (x2,y2)的直线上取一点(x0,x0x1−x2y1−y2+x1−xx2x1y2−x2y1)
- 过(x0,y0)的直线解析式为y=kx+y0−kx0
- 过(x0,x0x1−x2y1−y2+x1−x2x1y2−x2y1)的为y=kx+x0x1−x2y1−y2+x1−x2x1y2−x2y1−kx0
- 过(x1,y1)的为y=kx+y1−kx1
- 过(x2,y2)的为y=kx+y2−kx2
由(一)可得y0−kx0>x0x1−x2y1−y2+x1−x2x1y2−x2y1−kx0
k>x1−x2y1−y2(x0x1−x2y1−y2+x1−x2x1y2−x2y1−kx0)−(y1−kx1)=x1−x2x0y1−x0y2+x1y2−x1y1−k(x1−x0)=x1−x2(x0−x1)(y1−y2)−k(x0−x1)>x1−x2(x0−x1)(y1−y2)−x1−x2(x0−x1)(y1−y2)=0
k≤x1−x2y1−y2(x0x1−x2y1−y2+x1−x2x1y2−x2y1−kx0)−(y2−kx2)=x1−x2x0y1−x0y2+x2y2−x2y1−k(x2−x0)=x1−x2(x0−x2)(y1−y2)−k(x0−x2)≥x1−x2(x0−x2)(y1−y2)−x1−x2(x0−x2)(y1−y2)=0
- 综上所述,在y1−kx1和y2−kx2中一定存在一个数小于或等于x0x1−x2y1−y2+x1−x2x1y2−x2y1−kx0,又因为y0−kx0>x0x1−x2y1−y2+x1−x2x1y2−x2y1−kx0,所以在y1−kx1和y2−kx2中一定存在一个数小于y0−kx0,矛盾。
- 综上所述,此截距的最小值一定取在下凸包上。
- 证毕。
回归正题
现在我们知道了最优决策点一定在下凸包上
那么我们怎么找最优决策点呢?
首先我们易得下凸包中所有线的斜率一定是单调递增的
如果存在三个下凸包中的点(x1,y1),(x2,y2),(x3,y3)使得x1<x2<x3且x2−x1y2−y1>x3−x2y3−y2,则y2−x3−x1y3−y1x2−x3−x1x3y1−x1y3=x3−x1−x1y2+x1y3+x2y1−x2y3−x3y1+x3y2
又因为x1<x2<x3,所以x2−x1>0,x3−x2>0,x3−x1>0
故(y2−y1)(x3−x2)>(y3−y2)(x2−x1),即x2y1−x3y1+x3y2>x1y2−x1y3+x2y3
所以x3−x1−x1y2+x1y3+x2y1−x2y3−x3y1+x3y2>0,故y2>x3−x1y3−y1x2+x3−x1x3y1−x1y3,所以(x2,y2)一定不在下凸包内。
思路很清晰了吧?
简简单单的代码
#include<cstdio>
using namespace std;
const int N = 5e4 + 5;
int n, L, C, Qt[N], h = 1, t;
ll sum[N], f[N], Qx[N], Qy[N];
il ll sq(ll x) {return x * x;}
il double sl(ll x1, ll y1, ll x2, ll y2) {return (double) (y1 - y2) / (x1 - x2);}
int main() {
scanf("%d%d%d", &n, &L, &C);
sum[1] = C; f[1] = sq(C - L);
Qt[++t] = 0; Qx[t] = L + 1; Qy[t] = sq(Qx[t]);
Qt[++t] = 1; Qx[t] = L + 2 + C; Qy[t] = f[1] + sq(Qx[t]);
for(int i = 2; i <= n; ++i) {
scanf("%d", &C);
sum[i] = sum[i - 1] + C;
double slope = (i + sum[i]) << 1;
while(h < t && sl(Qx[h], Qy[h], Qx[h + 1], Qy[h + 1]) < slope) ++h;
f[i] = f[Qt[h]] + sq(i - Qt[h] - 1 + sum[i] - sum[Qt[h]] - L);
ll X = i + sum[i] + L + 1, Y = f[i] + sq(X);
while(h < t && sl(Qx[t], Qy[t], Qx[t - 1], Qy[t - 1]) >= sl(Qx[t], Qy[t], X, Y)) --t;
Qt[++t] = i; Qx[t] = X, Qy[t] = Y;
}
printf("%lld\n", f[n]);
return 0;
}问题来了
若Ck可以小于 0 呢?又该怎么做?
这个我们一眼就能看穿这玩意不满足单调性。
假如说考试的时候你不会证斜率的点或者决策有/没有单调性怎么办?
有两种方法。第一种是打表,多打几组。
第二种是不管三七二十一直接上不满足单调性时的做法。反正满足单调性的时候不满足单调性时的做法也能用。
不满足单调性的做法:
分治
我们用dc(l,r)表示计算[l,r]中的dpi。
对于左半边,我们先用dc(l,mid)算出[l,mid]中的dpi。然后我们就知道了所有的决策点,那么就可以建凸包。然后我们用这个凸包去更新[mid,r]中的dpi。这时的凸包是固定的,所以我们可以把[mid,r]的查询斜率排序,然后用单调队列维护。当然也可以直接在凸包上二分。
对于[mid,r]中的每个dpi,如果它的最优决策点在[1,mid],则上一步已经更新完,如果它的最优决策点不在[l,mid]我们也不需要[l,mid]的凸包。所以我们可以直接把左边的凸包抛掉,用dc(mid+1,r)计算之后的dpi。
T(n)=2T(2n)+O(nlogn))=O(nlog2n)
代码
#include <vector>
#include <stdio.h>
#include <string.h>
#include <algorithm>
int n, h[100005], w[100005], pre[100005];
long long dp[100005], sum[100005];
struct Point {
long long x, y;
int id;
Point(long long _x, long long _y, int _id): x(_x), y(_y), id(_id) {}
double operator/ (const Point &p) const { return (double) (y - p.y) / (x - p.x); }
};
long long min(long long a, long long b) { return a < b ? a : b; }
void cdq(int l, int r) {
while (l != r) {
std::vector<Point> Q, temp;
int mid = (l + r) >> 1;
cdq(l, mid);
for (int i = l; i <= mid; ++i)
temp.push_back(Point(h[i], dp[i] + (long long) h[i] * h[i] - sum[i], i));
std::sort(temp.begin(), temp.end(), [] (const Point &p1, const Point &p2) {
return p1.x == p2.x ? p1.y < p2.y : p1.x < p2.x;
});
Q.push_back(temp[0]); int _size = 0;
for (int i = 1; i < (int) temp.size(); ++i) {
if (Q[_size].x == temp[i].x) continue;
while (_size && Q[_size] / Q[_size - 1] > Q[_size] / temp[i]) Q.pop_back(), --_size;
Q.push_back(temp[i]); ++_size;
}
for (int i = r; i > mid; --i) {
int l = 1, r = Q.size() - 1, sl = h[i] << 1;
while (l <= r) {
int mid = (l + r) >> 1;
if (Q[mid] / Q[mid - 1] > sl) r = mid - 1;
else l = mid + 1;
}
int k = Q[r].id;
dp[i] = min(dp[i], dp[k] + (long long) (h[i] - h[k]) * (h[i] - h[k]) + sum[i - 1] - sum[k]);
}
l = mid + 1;
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", h + i);
for (int i = 1; i <= n; ++i) scanf("%d", w + i), sum[i] = sum[i - 1] + w[i];
memset(dp, 0x3f, sizeof dp); dp[1] = 0;
cdq(1, n); printf("%lld\n", dp[n]);
return 0;
}平衡树
思路很简洁,一说就懂,一写就废
代码
#include <stdio.h>
#include <string.h>
inline unsigned rand() {
static unsigned seed = 19260817;
return (seed = seed * 1279u + 10001279u) ^= (seed >> 7);
}
struct Point {
long long x, y;
int id;
Point(long long _x, long long _y, int _id): x(_x), y(_y), id(_id) {}
Point() {}
double operator/ (const Point &p) const { return (double) (y - p.y) / (x - p.x); }
};
struct Treap {
struct node {
int ls, rs, size;
Point p;
double lp, rp;
unsigned key;
} tr[100005];
int cnt, root;
inline int new_node(const Point &p) {
tr[++cnt].p = p;
tr[cnt].key = rand();
tr[cnt].size = 1;
return cnt;
}
inline void push_up(int k) { if (k) tr[k].size = tr[tr[k].ls].size + tr[tr[k].rs].size + 1; }
void rotate_left(int &k) {
int old_k = k;
k = tr[k].rs;
tr[old_k].rs = tr[k].ls;
tr[k].ls = old_k;
push_up(old_k);
push_up(k);
}
void rotate_right(int &k) {
int old_k = k;
k = tr[k].ls;
tr[old_k].ls = tr[k].rs;
tr[k].rs = old_k;
push_up(old_k);
push_up(k);
}
int insert(int &k, const Point &v) {
int tmp;
if (!k) { return k = new_node(v); }
if (v.x < tr[k].p.x) {
if (tmp = insert(tr[k].ls, v)) {
if (tr[k].key > tr[tr[k].ls].key) rotate_right(k);
push_up(k);
return tmp;
} else return 0;
} else if (v.x > tr[k].p.x) {
if (tmp = insert(tr[k].rs, v)) {
if (tr[k].key > tr[tr[k].rs].key) rotate_left(k);
push_up(k);
return tmp;
} else return 0;
} else {
if (tr[k].p.y < v.y) return 0;
tr[k].p.y = v.y; tr[k].p.id = v.id; return k;
}
}
void remove(int &k, long long x) {
if (!k) return;
if (tr[k].p.x == x) {
if (tr[k].ls && tr[k].rs) {
if (tr[tr[k].ls].key < tr[tr[k].rs].key) rotate_right(k), remove(tr[k].rs, x);
else rotate_left(k), remove(tr[k].ls, x);
} else k = tr[k].ls | tr[k].rs;
} else if (x < tr[k].p.x) remove(tr[k].ls, x);
else remove(tr[k].rs, x);
push_up(k);
}
int rank(long long x) {
int rnk = 0, k = root;
while (k) {
if (x <= tr[k].p.x) k = tr[k].ls;
else rnk += tr[tr[k].ls].size + 1, k = tr[k].rs;
}
return rnk + 1;
}
int value(int x) {
if (x > tr[root].size || x <= 0) return -1;
int k = root;
while (k) {
if (x <= tr[tr[k].ls].size) k = tr[k].ls;
else if (x == tr[tr[k].ls].size + 1) return k;
else x -= tr[tr[k].ls].size + 1, k = tr[k].rs;
}
return -1;
}
int prev(long long v) { return value(rank(v) - 1); }
int next(long long v) { return value(rank(v + 1)); }
void insert_hull(const Point &point) {
int k = insert(root, point);
if (!k) return;
int k1 = prev(point.x);
if (k1 != -1) {
while (tr[k1].lp > point / tr[k1].p) remove(root, tr[k1].p.x), k1 = prev(tr[k1].p.x);
tr[k].lp = tr[k1].rp = point / tr[k1].p;
} else tr[k].lp = -1e30;
int k2 = next(point.x);
if (k2 != -1) {
while (point / tr[k2].p > tr[k2].rp)
remove(root, tr[k2].p.x), k2 = next(tr[k2].p.x);
tr[k].rp = tr[k2].lp = tr[k2].p / point;
} else tr[k].rp = 1e30;
if (tr[k].lp > tr[k].rp) {
remove(root, tr[k].p.x);
tr[k1].rp = tr[k2].lp = tr[k1].p / tr[k2].p;
}
}
int query_hull(long long slope) {
int k = root;
while (k) {
if (tr[k].lp <= slope && slope <= tr[k].rp) return tr[k].p.id;
else if (slope < tr[k].lp) k = tr[k].ls;
else k = tr[k].rs;
}
return -1;
}
} treap;
int n, w[100005], h[100005];
long long sum[100005], dp[100005];
long long min(long long a, long long b) { return a < b ? a : b; }
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", h + i);
for (int i = 1; i <= n; ++i) scanf("%d", w + i), sum[i] = sum[i - 1] + w[i];
memset(dp, 0x3f, sizeof dp); dp[1] = 0;
treap.new_node(Point(h[1], (long long) h[1] * h[1] - w[1], 1));
treap.root = 1; treap.tr[1].lp = -1e30; treap.tr[1].rp = 1e30;
for (int i = 2; i <= n; ++i) {
int j = treap.query_hull(h[i] << 1);
dp[i] = min(dp[i], dp[j] + (long long) (h[i] - h[j]) * (h[i] - h[j]) + sum[i - 1] - sum[j]);
treap.insert_hull(Point(h[i], dp[i] + (long long) h[i] * h[i] - sum[i], i));
}
printf("%lld", dp[n]);
return 0;
}二进制分组
我们将所有的点分成若干组,第i组大小为2i,显然组数不超过O(logn)。我们维护每组的凸包。
插入一个点时,若没有第 0 组,则将它作为第 0 组,否则将它和第 0 组合并。这样我们得到了第 1 组。接下来如果有第 1 组,则再将它与第 1 组合并得到第 2 组……类似二进制+1 的过程。
查询在每一组分别二分,取最大即可。
关于时间复杂度:
显然每个点最多被合并O(logn)次。我们合并两个包含O(n)个节点的凸包的时间复杂度是O(n)的,故均摊到每个点上合并的时间复杂度是O(1),又因为共有O(n)个点,所以总时间复杂度O(nlogn)。
代码
#include <string.h>
#include <stdio.h>
#include <vector>
int n, h[100005], w[100005];
long long dp[100005], sum[100005];
struct Point {
long long x, y;
int id;
Point(long long _x, long long _y, int _id): x(_x), y(_y), id(_id) {}
double operator/ (const Point &p) const { return (double) (y - p.y) / (x - p.x); }
};
struct ConvexHull {
std::vector<Point> p;
void merge(ConvexHull &h) {
std::vector<Point> possible_conv;
int i = 0, j = 0;
while (i < (int) p.size() && j < (int) h.p.size())
if (p[i].x == h.p[j].x) {
if (p[i].y < h.p[j].y) possible_conv.push_back(p[i]);
else possible_conv.push_back(h.p[j]);
++i; ++j;
} else if (p[i].x < h.p[j].x) possible_conv.push_back(p[i]), ++i;
else possible_conv.push_back(h.p[j]), ++j;
while (i < (int) p.size()) possible_conv.push_back(p[i]), ++i;
while (j < (int) h.p.size()) possible_conv.push_back(h.p[j]), ++j;
p.clear(); p.push_back(possible_conv[0]);
int _size = 0;
for (int i = 1; i < (int) possible_conv.size(); ++i) {
while (_size && p[_size] / p[_size - 1] > p[_size] / possible_conv[i]) p.pop_back(), --_size;
p.push_back(possible_conv[i]); ++_size;
}
h.p.clear();
}
int query(long long k) {
int l = 1, r = p.size() - 1;
while (l <= r) {
int mid = (l + r) >> 1;
if (p[mid] / p[mid - 1] > k) r = mid - 1;
else l = mid + 1;
}
return p[r].id;
}
ConvexHull() {}
ConvexHull(const Point &P) { p.push_back(P); }
} conv[17];
long long min(long long a, long long b) { return a < b ? a : b; }
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", h + i);
for (int i = 1; i <= n; ++i) scanf("%d", w + i), sum[i] = sum[i - 1] + w[i];
memset(dp, 0x3f, sizeof dp); dp[1] = 0;
conv[0] = ConvexHull(Point(h[1], (long long) h[1] * h[1] - w[1], 1));
for (int i = 2; i <= n; ++i) {
for (int j = 0; j < 17; ++j) {
if (conv[j].p.empty()) continue;
int k = conv[j].query(h[i] << 1);
dp[i] = min(dp[i], dp[k] + (long long) (h[i] - h[k]) * (h[i] - h[k]) + sum[i - 1] - sum[k]);
}
ConvexHull cv(Point(h[i], dp[i] + (long long) h[i] * h[i] - sum[i], i));
for (int j = 0; j < 17; ++j) {
if (conv[j].p.empty()) {
conv[j].p = cv.p;
break;
}
cv.merge(conv[j]);
}
}
printf("%lld", dp[n]);
return 0;
}总结
在dp的最小/最大化问题中,将转移方程分成四部分:一部分与i,j都无关,一部分只与j有关,一部分只与i有关,还有一部分和i,j都有关。如果它能写成 y=kx+b 的形式,我们就可以维护一个凸包,来进行状态的转移。
练习
此处放出你谷的链接
更新日志
7ced7-Reuploads previous blogs于